Toán 10 bài hàm số bậc hai
Qua bài học này, các bạn sẽ biết dạng hàm số bậc hai và phương pháp khảo sát hàm số bậc hai. Đây là dạng toán quan trọng trong chương trình toán lớp 10 và sẽ có trong nội dung ôn tập thi học kỳ và kiểm tra.
Bạn đang xem: Toán 10 bài hàm số bậc hai
1. Tóm tắt lý thuyết
1.1. Định nghĩa
1.2. Đồ thị hàm số bậc hai
1.3. Sự biến thiên của hàm số bậc hai
2. Bài tập minh hoạ
3.Luyện tập bài 3 chương 2đại số 10
3.1. Trắc nghiệm về hàm sốbậc hai
3.2. Bài tập SGK & Nâng cao về hàm sốbậc hai
4.Hỏi đáp vềbài 3 chương 2đại số 10
Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng\(y = a{x^2} + bx + c\)trong đó a, b, c là các hằng số cho trước và\(a \ne 0\).Tập xác định của hàm số bậc hai là R.Hàm số\(y=ax^2\)(a khác 0) mà chúng ta đã học ở lớp dưới là một hàm số bậc hai có đồ thị là một Parabol.
a) Nhắc lại về đồ thị\(y=ax^2(a\ne0)\)Đồ thị luôn đi qua gốc tọa độ\(O(0;0).\)Parabol đối xứng nhau qua trục tung.Parabol hướng lên trên khi a dương, và hướng xuống dưới khi a âm.b) Đồ thị hàm số\(y=ax^2+bx+c(a\ne0)\)
Ta biết rằng:
\(\begin{array}{l} a{x^2} + bx + c = a\left( {{x^2} + 2\frac{b}{{2x}} + \frac{{{b^2}}}{{4{a^2}}}} \right) - \frac{{{b^2}}}{{4{a^2}}} + c\\ = a{\left( {x + \frac{b}{{2a}}} \right)^2} - \frac{{{b^2} - 4ac}}{{4a}} \end{array}\)Vì vậy, nếu đặt:\(\Delta = {b^2} - 4ac;p = - \frac{b}{{2a}};q = - \frac{\Delta }{{4a}}\)
Thì hàm số\(y=ax^2+bx+c(a\ne0)\)trở thành\(y = a{\left( {x - p} \right)^2} + q\)
Kết luận:
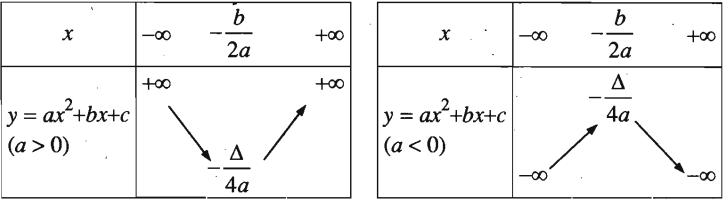
Đồ thị hàm số\(y=ax^2+bx+c(a\ne0)\)là một Parabol có đỉnh\(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\), nhận đường thẳng\(x = - \frac{b}{{2a}}\)làm trục đối xứng và hướng bề lõm lên trên khi a dương, bề lõm xuống dưới khi a âm.
1.3. Sự biến thiên của hàm số bậc hai
Bài tập minh họa
Ví dụ 1:
Xác định parabol \(\left( P \right)\): \(y = a{x^2} + bx + c\), \(a \ne 0\) biết \(\left( P \right)\) đi qua \(A(2;3)\) có đỉnh \(I(1;2)\).
Hướng dẫn:Vì \(A \in \left( P \right)\) nên \(3 = 4a + 2b + c\) (1).
Xem thêm: Giá Xe 7 Chỗ Xpander Giá Bao Nhiêu, Giá Xe Mitsubishi Xpander Mới Nhất Tháng 10/2021
Mặt khác \(\left( P \right)\) có đỉnh \(I(1;2)\) nên \( - \frac{b}{{2a}} = 1 \Leftrightarrow 2a + b = 0\) (2) và \(I \in \left( P \right)\) suy ra \(2 = a + b + c\) (3)
Từ (1), (2) và (3) ta có \(\left\{ \begin{array}{l}4a + 2b + c = 3\\2a + b = 0\\a + b + c = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\\c = 3\end{array} \right.\)
Vậy \(\left( P \right)\) cần tìm là \(y = {x^2} - 2x + 3\).
Ví dụ 2:Xác định parabol \(\left( P \right)\): \(y = a{x^2} + bx + c\), \(a \ne 0\) biết Hàm số \(y = a{x^2} + bx + c\) có giá trị nhỏ nhất bằng \(\frac{3}{4}\) khi \(x = \frac{1}{2}\) và nhận giá trị bằng \(1\) khi\(x = 1\).
Hướng dẫn:Hàm số \(y = a{x^2} + bx + c\) có giá trị nhỏ nhất bằng \(\frac{3}{4}\) khi \(x = \frac{1}{2}\) nên ta có:
\( - \frac{b}{{2a}} = \frac{1}{2} \Leftrightarrow a + b = 0\) (5)\(,\,\,\frac{3}{4} = a{\left( {\frac{1}{2}} \right)^2} + b\left( {\frac{1}{2}} \right) + c \Leftrightarrow a + 2b + 4c = 3\) (6) và \(a > 0\)
Hàm số \(y = a{x^2} + bx + c\) nhận giá trị bằng \(1\) khi\(x = 1\) nên \(a + b + c = 1\)(7)
Từ (5), (6) và (7) ta có \(\left\{ \begin{array}{l}a + b = 0\\a + 2b + 4c = 3\\a + b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 1\\c = 1\end{array} \right.\)
Vậy \(\left( P \right)\) cần tìm là \(y = {x^2} - x + 1\).
Ví dụ 3:Lập bảng biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = {x^2} + 3x + 2\)
b) \(y = - {x^2} + 2\sqrt 2 x\)
Hướng dẫn:a) Ta có \( - \frac{b}{{2a}} = - \frac{3}{2},\,\, - \frac{\Delta }{{4a}} = - \frac{1}{4}\)
Bảng biến thiên:
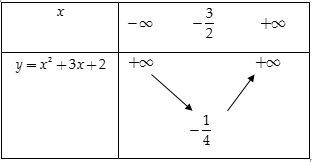
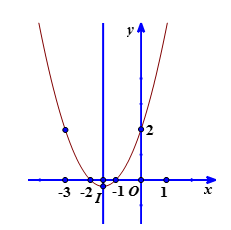
Suy ra đồ thị hàm số \(y = {x^2} + 3x + 2\) có đỉnh là \(I\left( { - \frac{3}{2}; - \frac{1}{4}} \right)\), đi qua các điểm \(A\left( { - 2;0} \right),\,\,B\left( { - 1;0} \right),\,\,C\left( {0;2} \right),\,\,D\left( { - 3;2} \right)\)
Nhận đường thẳng \(x = - \frac{3}{2}\) làm trục đối xứng và hướng bề lõm lên trên.
b) Ta có \( - \frac{b}{{2a}} = \sqrt 2 ,\,\, - \frac{\Delta }{{4a}} = 2\)
Bảng biến thiên:
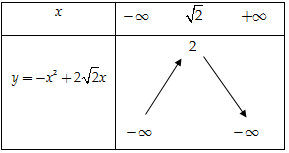
Suy ra đồ thị hàm số \(y = - {x^2} + 2\sqrt 2 x\) có đỉnh là \(I\left( {\sqrt 2 ;2} \right)\), đi qua các điểm \(O\left( {0;0} \right),\,\,B\left( {2\sqrt 2 ;0} \right)\)











